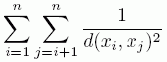
Audze-Eglais Designs

Audze-Eglais designs are obtained by minimizing the following objective:

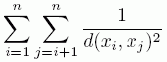
where d(xi; xj) is the Euclidean distance between points xi and xj and n is the number of design points. The criterion was first introduced by Audze and Eglais (1977) and is based on the analogy of minimizing forces between charged particles. In Bates et al. (2004), the problem of finding Audze-Eglais LHDs is formulated and a permutation genetic algorithm is used to generate them. Liefvendahl and Stocki (2006) compare maximin and Audze-Eglais LHDs and recommend the Audze-Eglais criterion over the maximin criterion. Examples of practical applications of Audze-Eglais LHDs can be found in Rikards et al. (2001), Bulik et al. (2004), Stocki (2005), and Hino et al. (2006).

•Audze, P. and V. Eglais (1977). New approach for planning out of experiments, Problems of Dynamics and Strengths, 35, 104-107.
•Bates, S.J., J. Sienz, and V.V. Toropov (2004). Formulation of the optimal Latin hypercube design of experiments using a permutation genetic algorithm, AIAA 2004-2011, 1-7. View article
•Bulik, M., M. Liefvendahl, R. Stocki, and C. Wauquiez (2004). Stochastic simulation for crashworthiness, Advances in Engineering Software, 35 (12), 791-803. View article
•Hino, R., F. Yoshida, and V.V. Toropov (2006). Optimum blank design for sheet metal forming based on the interaction of high-and low-fidelity FE models, Archive of Applied Mechanics, 75 (10), 679-691. View article View site of author
•Liefvendahl, M. and R. Stocki (2006). A study on algorithms for optimization of Latin hypercubes, Journal of Statistical Planning and Inference, 136 (9), 3231-3247. View article
•Rikards, R., A. Chate, and G. Gailis (2001). Identification of elastic properties of laminates based on experiment design, International Journal of Solids and Structures, 38 (30-31), 5097-5115. View article View site of author
•Stocki, R. (2005). A method to improve design reliability using optimal Latin hypercube sampling, Computer Assisted Mechanics and Engineering Sciences, 12 (4), 393-412. View article View site of author